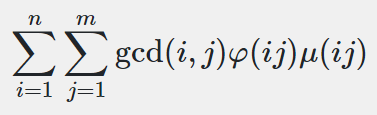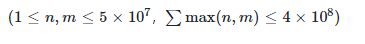因为已经半退役状态好久了,曩昔辉煌状态不复存焉,遽寻良方,遂行此道。
需要完全学会问题。摘选有意思的问题。
从 2023/9/1 开始。
2023/9/1
Q1
保留||bloodstalk 2023/9/1 7:48:12
vuqa
这个式子怎么推啊/kel
保留||bloodstalk 2023/9/1 8:12:33
时间限制:14s
考虑到当 $i, j$ 互质时,里面的单项式变成 $\varphi(ij)\mu(ij)=\varphi(i)\mu(i)\varphi(j)\mu(j)$ ;而若不互质,由于有 $\mu(i,j)$ ,里面单项式值为 $0$ 。故 $\gcd$ 可以去掉。
令 $f(k)=\varphi(k)\mu(k)d(k)$ ,显然原式为 $\sum_{k=1}^{nm}f(k)$ 。现在分析 $f(k)$ :
考虑 $\mu(k)\ne0$ 的情况,令 $k=\prod_{i=1}^c p_i$ ,其中 $p_i$ 表示其中第 $i$ 个质因子, $c$ 表示质因子个数,
$$\begin{aligned}f(k)&=k\left(\prod_{i=1}^c\dfrac{p_i-1}{p_i}\right)\cdot(-1)^c\cdot2^c\\ &=(-2)^c\prod_{i=1}^c(p_i-1)\end{aligned}$$
显然积性。然后发现这样做不了范围大于开方的部分,乐。数据范围小点倒是可以做。
回到之前,式子化为
$$\begin{aligned}&\quad\sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)=1]\varphi(ij)\mu(ij)\\&=\sum\sum\sum_{d|\gcd(i,j)}\mu(d)\varphi(ij)\mu(ij)\\ &=\sum_{d=1}^{\max(n,m)}\mu(d)\left(\sum_{i=1}^{\left\lfloor\frac{n}{d}\right\rfloor}\varphi(id)\mu(id)\right)\left(\sum_{j=1}^{\left\lfloor\frac{m}{d}\right\rfloor}\varphi(jd)\mu(jd)\right) \end{aligned}$$
对味了。用狄利克雷前缀和即可,时间复杂度 $\mathcal{O}(n\log\log n)$ 。
在 Mathematics Stack Exchange 上找到了类似问题。这个结论也可以记记:
$$\sum_{d|n}\mu(d)\varphi(d)=\prod_{i=1}^c(2-p_i) $$
$$\sum_{d|n}\mu^2(d)\varphi^2(d)=\prod_{i=1}^c\left(1+(p_i-1)^2\right) $$
$$\sum_{d|n}\frac{\mu(d)}{\varphi(d)}=\prod_{i=1}^c\frac{p_i-2}{p_i-1} $$
Q2
Register_int 2023/9/1 8:14:39
哦对了
不知道多少年前51nod VP 有一个阴间题
想问下做法
CF1146H,n<=2e3
二维平面上有 $n~(5\leq n\leq300)$ 个点,其中第 $i$ 个点的坐标是 $(x_i,y_i)$ 。
你想找出来五个点,使得这五个点形成一个五角星,五角星定义为五条对角线互相交于五个点。
求找出来五个点的方案数。
正好原题还没做。
不会计算几何哇!学习啦。可以看出问题其实就是要找 5 个顶点的凸包个数。设 $f_{i,j,k}$ 表示 $i$ 到 $j$ 路径长度为 $k$ 的路径个数,用极角排序可以保证凸包。
至于 n<=2e3……似乎没有 $n^3$ 以下的做法。