部分确定有限状态自动机总结

一些记号

  • 子串 $s_{i\cdots j}=s_is_{i+1}\cdots s_{j}$ 。
  • 前缀 $\mathrm{pre}(s,x)=s_{0\cdots x}$ 。
  • 后缀 $\mathrm{suf}(s,x)=s_{\mathrm{len}-x\cdots \mathrm{len}-1}$ 。

确定有限状态自动机

自动机是一个对信号序列进行判定的 数学模型：给定一串信号，会给出是或不是的答案。

确定有限状态自动机 是其中一种自动机，由五部分构成：

  1. 字符集（ $\Sigma$ ）。
  2. 状态集合（ $Q$ ），在有向图中相当于每个结点。
  3. 起始状态（ $s$ ），自动机判定时初始的状态，在有向图中相当于起点。
  4. 接受状态集合（ $F$ ）， $F\subseteq Q$ ，自动机判定时的“终点集合”，若字符串最终判定到 $F$ 中的状态，则返回 $\mathrm{True}$ ，否则返回 $\mathrm{False}$ 。
  5. 转移函数（ $\delta$ ）， $\delta(i,c)$ 在有向图中表示结点 $i$ 的 $c$ 字符指向的结点，若没有所指结点，则为 $\mathrm{null}$ 。

下图自动机 $s$ 点位起始状态、红点为接受状态，此自动机接受且仅接受字符串 $\texttt{a},\texttt{ab},\texttt{aac}$ 。

字典树

一种树形的自动机。

下图是字符串集合 $\{\texttt{abac},\texttt{abcca},\texttt{acba},\texttt{acbb},\texttt{bacb}\}$ 的字典树：

构建与查找

int tot = 1;
bool end[N];
struct TRIE {
	int op, arr[26];
	TRIE () {
		op = 0;
		memset(arr, 0, sizeof(arr));
	}
}trie[N];

void insert(char* st) {
	int len = strlen(st), p = 1;
	for(int i = 0; i < len; i++) {
		int c = st[i] - 'a';
		if (trie[p].arr[c] == 0) 
			trie[p].arr[c] = ++tot;
		p = trie[p].arr[c];
	}
	end[p] = 1;
}

int search(char* st) {
	int len = strlen(st), p = 1;
	for (int i = 0; i < len; i++) {
		int c = st[i] - 'a';
		if (!trie[p].arr[c])
			return 0;
		p = trie[p].arr[c]; 
	}
	if(!end[p]) return 0;
	if(!trie[p].op) {
		trie[p].op++;
		return 1;
	} 
	return 2;
}

KMP 自动机

周期和 border

若 $0<p\leq|s|，s_i=s_{i+p},\forall i\in\{1,\cdots,|s|-p\}$ ，就称 $p$ 是 $s$ 的 周期（period）。

若 $0\leq r<|s|，\mathrm{pre}(s,r)=\mathrm{suf}(s,r)$ ，就称 $\mathrm{pre}(s,r)$ 是 $s$ 的 border。

“ $\mathrm{pre}(s,r)$ 是 $s$ 的 border”是“ $|s|-r$ 是 $s$ 的周期”的充要条件。

KMP 算法可以在 $\mathcal{O}(n)$ 时间求出前缀的最大 border 长度数组 $\pi_i$ 作为失配链接。

KMP 自动机的原理与构建

KMP 自动机依赖于 border，考虑分析 border 的作用。因为 border 既是字符串前缀，也是字符串后缀，所以若在判定字符串时失配，border 可以“纠正”判定字符串和自动机的匹配位置。而自身 border 的 border 一定是自身的 border，通过遍历 $\pi_i,\pi_{\pi_i},\pi_{\pi_{\pi_i}},\cdots$ 就能枚举 border。

KMP 自动机的接受状态为末尾的状态，转移函数如下：

$$\delta(i, c)= \begin{cases} i+1&s_{i+1}=c\\ 0&s_1\ne c\land i=0\\ \delta(\pi_i,c)&s_{i+1}\ne c\land i>0 \end{cases} $$

这个转移函数不但判定的时候适用，而且求 $\pi_i$ 数组时也适用。

由于 KMP 自动机可以看作是链状的，所以只用一维数组维护就好了。

void BuildKMP(char *s, int len) {
	fail[0] = 0;                           // fail 为失配指针
	for (int i = 1, j = 0; i < len; i++) {
		while(j && s[i] != s[j]) j = fail[j];
        if (s[i] == s[j]) j++;
		fail[i] = j;
	}
}

void Judge(char *auto, int autoLen, char *s, int len) {
	for (int i = 0, j = 0; i < len; i++) {
		while(j && s[i] != auto[j]) j = fail[j];
		if(s[i] == auto[j])	j++;
		if(j == autoLen) { /* 接受 */ } 
	}
}

AC 自动机

上文的 KMP 自动机由一个字符串构建，现在我们考虑扩展到多个字符串，于是很自然地想到把 KMP 自动机放到字典树上，这就是 AC 自动机。

字典图

可以说，KMP 自动机是特殊的 AC 自动机，AC 自动机的状态的意义、起始状态、接受状态、转移函数都和 KMP 自动机相同，比如 AC 自动机的转移函数为

$$\delta_{\text{AC}}(i, c)= \begin{cases} \delta_{\text{trie}}(i, c)&\delta_{\text{trie}}(i, c)\ne \mathrm{null}\\ \mathrm{root}&\delta_{\text{trie}}(i, c)=\mathrm{null}\land i=\mathrm{root}\\ \delta_{\text{AC}}(\pi_i,c)&\delta_{\text{trie}}(i, c)=\mathrm{null}\land i\ne\mathrm{root} \end{cases} $$

与 KMP 自动机转移函数相同。

但是由于每次失配时需要使用失配指针，每次输入一个字符时经过的节点数不确定，时间复杂度可能会退化。那么考虑对字典树的结构进行优化：预处理出每一个状态可能转移到的所有状态，具体地，AC 自动机的转移函数不变，但是当 $\delta_{\text{trie}}(i, c)=\mathrm{null}\land i\ne\mathrm{root}$ 时， $\delta_{\text{trie}}(i, c)$ 直接指向 $\delta_{\text{AC}}(\pi_i, c)$ 。

namespace AC {
	int t[N][30], e[N], fail[N];
	int tot;
	void Insert(char *s) {  // 建立字典树
		int p = 0, len = strlen(s);
		for (int i = 0; i < len; i++) {
			int ch = s[i] - 'a';
			if (!t[p][ch]) t[p][ch] = ++tot;
			p = t[p][ch];
		}
		e[p]++;
	}
	queue <int> q;
	void Build() {  // 在字典树上构建 AC 自动机
		while(!q.empty()) q.pop();
		for (int i = 0; i < 26; i++)
			if (t[0][i]) q.push(t[0][i]);
		while (!q.empty()) {
			int p = q.front(); q.pop();
			for (int i = 0; i < 26; i++)
				if (t[p][i])
					fail[t[p][i]] = t[fail[p]][i], q.push(t[p][i]);
				else
					t[p][i] = t[fail[p]][i];  // 优化，字典树变成字典图
		}
	}
}

后缀自动机

顾名思义，后缀自动机就是“后缀”的“自动机”，那么把一个字符串的每个后缀都插入到一个字典树上，这就是一个后缀自动机，如下图为 $\texttt{aabaabbc}$ 的后缀字典树。

这显然是有缺陷的，其状态数是平方级别的，有很多状态都是冗余的，比如状态 $4$ 和 $7$ 是等价的，可以缩在一起。那么我们考虑怎么压缩后缀字典树。

结尾集合

记一个子串 $p$ 在字符串 $s$ 的结尾位置集合为 $\mathrm{endpos}(p)$ ，例如当 $s=\texttt{aabaabbc}$ 时， $\mathrm{endpos}(\texttt{ab})=\{2,5\}$ 。

结尾集合具有很多性质：

  1. 如果两个非空子串的结尾集合相同，则其中一个子串必为另一个子串的后缀，而且它们在后缀字典树上的状态是等价的。例如 $\mathrm{endpos}(\texttt{aab})=\mathrm{endpos}(\texttt{ab})$ ，它们在后缀字典树上的状态分别为 $7,4$ 。像这样等价的状态（结尾集合相同的子串），我们把它们归为一个 等价类。
  2. 对于两个非空子串 $u,v$ ，其中 $|u|\leq|v|$ ，那么它们的结尾集合的关系如下：

$$\begin{cases} \operatorname{endpos}(v) \subseteq \operatorname{endpos}(u) & \text{if } u \text{ is a suffix of } v \\ \operatorname{endpos}(v) \cap \operatorname{endpos}(u) = \varnothing & \text{otherwise} \end{cases} $$

我们将等价类作为后缀自动机的状态，等价类个数是 $\mathcal{O}(n)$ 的，大大优化了时空。

失配指针

记 $\mathrm{fail}(u)$ 指向等价类 $u$ 中的最长串的 不在当前等价类里的最长后缀 所在等价类。

又因为性质 2，所以各个等价类由失配指针形成一棵树，我们称这棵树为 parent tree（也可以叫 fail tree、link tree 等等）。

如图为 $\texttt{aabaabbc}$ 的后缀自动机，其中蓝边为失配指针。

记 $\mathrm{longest}(u)$ 表示等价类 $u$ 中的最长串长度， $\mathrm{shortest}(u)$ 表示等价类 $u$ 中的最短串长度。引出结尾集合的第三个性质：

  1. $\mathrm{longest}(\mathrm{fail}(u))+1=\mathrm{shortest}(u)$ ，在自动机的状态上要维护结尾集合是很困难的，我们只用考虑维护状态的最长串长度而不用记录结尾集合，而最短串长度可以有这条性质推出来（顺带一提：如果题目中确实需要结尾集合的，可以用可持久化线段树维护）。

后缀自动机的构建

可参考后缀自动机构建可视化学习。

后缀自动机和之前的自动机一样都是增量构造：先构造 $s_{0\cdots n-1}$ ，在此基础上再插入 $s_{n}$ ，构建新的自动机。我们定义末尾状态 $\mathrm{last}$ 表示构造完 $s_{0\cdots n}$ 后，子串 $s_{0\cdots n}$ 在后缀自动机对应的状态。

插入一个新字符 $c$ ：

  1. 从 $\mathrm{last}$ 顺着失配指针链找，找到末尾状态最长的后缀状态 $p$ ，使得其可以添加这个字符 $c$ ，假设它可以通过 $c$ 转移到 $q$ 。
  2. 新建状态 $np$ 表示当前后缀。从 $\mathrm{last}$ 到 $p$ 的路径上，原本遇到 $c$ 会失配的状态，现在可以转移到 $np$ 。
  3. 新增字符后， $q$ 由 $p$ 而来的子串的结尾集合和原本 $q$ 包含的子串的结尾集合不相同，发生冲突。
  4. 既然冲突，那么就把 $q$ 拆出新节点 $nq$ ， $\mathrm{fail}(nq)$ 指向原本的 $\mathrm{fail}(q)$ ，而让 $\mathrm{fail}(q)$ 指向 $nq$ 。同时 $p$ 的失配指针链上通过 $c$ 转移到 $q$ 的边全部重定向至 $nq$ 。

只要把图记住就好说了。

namespace SAM {
	int Last, tot;
	int fail[N], maxlen[N];
	int trans[N][26];
	void Build() { Last = tot = 1; }
	void Insert(int c) {
		int p = Last, np = ++tot;
		maxlen[np] = maxlen[p] + 1;
		for (; p && !trans[p][c]; p = fail[p])
			trans[p][c] = np;
		if (!p) fail[np] = 1;
		else {
			int q = trans[p][c];
			if (maxlen[q] == maxlen[p] + 1) fail[np] = q;
			else {
				int nq = ++tot; fail[nq] = fail[q];
				memcpy(trans[nq], trans[q], 26 << 2);
				maxlen[nq] = maxlen[p] + 1;
				for (; p && trans[p][c] == q; p = fail[p])
					trans[p][c] = nq;
				fail[np] = fail[q] = nq;
			}
		}
		Last = np;
	}
}

后缀自动机基本应用

  1. $\mathcal{O}(n)$ 求后缀数组，所以后缀数组能做的题，如果不卡空间，后缀自动机都能做。
  2. 判断模式串是否出现，从初始结点开始转移即可。
  3. 求本质不同子串个数， $\mathrm{longest}(u)-\mathrm{longest}(\mathrm{fail}(u))$ 。
  4. 字典序第 k 大子串。

广义后缀自动机

KMP 自动机与 AC 自动机的关系就是后缀自动机与广义后缀自动机的关系。所以我们把多个串的字典树建立好，再在它们上面建立后缀自动机就是广义后缀自动机了。

namespace GSAM {
	int tot = 1;
	int trans[N][26];
	int fail[N], maxlen[N];

	int extend (int c, int p) {
		int np = trans[p][c];
		if (maxlen[np]) return np;
		maxlen[np] = maxlen[p] + 1;
		for (p = fail[p]; p && !trans[p][c]; p = fail[p]) trans[p][c] = np;
		if (!p) fail[np] = 1;
		else {
			int q = trans[p][c];
			if (maxlen[q] == maxlen[p] + 1) fail[np] = q;
			else {
				int nq = ++tot; fail[nq] = fail[q];
				for (int i = 0; i < 26; i++) 
					trans[nq][i] = maxlen[trans[q][i]]? trans[q][i]: 0;
				maxlen[nq] = maxlen[p] + 1;
				for (; p && trans[p][c] == q; p = fail[p]) trans[p][c] = nq;
				fail[np] = fail[q] = nq;
			}
		}
		return np;
	}
	
	void Insert(char *s) {
		int p = 1;
		for(int i = 0; s[i]; i++) {
			if (!trans[p][s[i] - 'a'])
				trans[p][s[i] - 'a'] = ++tot;
			p = trans[p][s[i] - 'a'];
		}
	}

	struct node {
		int x, Last;
	};
	void Build() {
		queue<node> q;
		for (; !q.empty(); q.pop());
		for (int i = 0; i < 26; i++)
			if(trans[1][i]) q.push((node){ i, 1 });
		while(!q.empty()) {
			node u = q.front(); q.pop();
			int lst = extend(u.x, u.Last);
			for (int i = 0; i < 26; i++)
				if(trans[lst][i]) q.push((node){ i, lst });
		}
	}
}

回文自动机

回文自动机，又称回文树，也可以处理部分回文类问题。

回文树是由两棵分别为奇、偶的树构成的森林。

其中，奇树用于存储长度为奇数的回文串；偶树用于存储长度为偶数的回文串。

每个节点可以维护该节点字符串长度、该节点出边连接到的节点、失配指针。

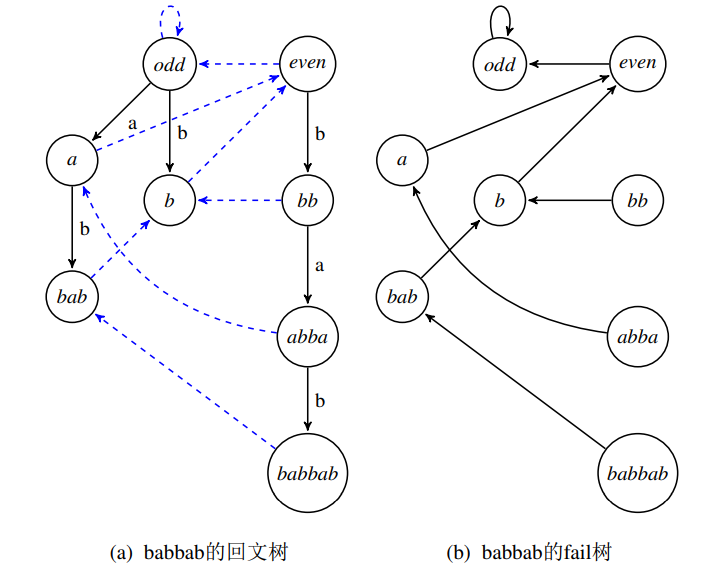
回文自动机的构造

引理：以新加入的字符 $c$ 为结尾的，未在 $s$ 中出现过的回文子串最多只有 $1$ 个，且必为 $s+c$ 的最长回文后缀。 那么构造时，求出 $s+c$ 的最长回文后缀即可。于是现在要在 $s$ 的最长回文后缀对应的失配链中找到长度最大的一个节点 $t$ ，使得 $s_{|s|-\mathrm{len}(t)}=c$ ，则 $sc$ 的最长回文后缀即为 $ctc$ 。

也因此，新建节点时的失配指针要连向最长的 $t$ 满足 $s_{|s|-\mathrm{len}(t)}=c$ 的节点，若 $\mathrm{len}(t)=-1$ 则连偶树根。

namespace PAM {
	int len[N], fail[N], s[N], trans[N][27];
	int Last, tot = -1, n = 0;
	int sum[N];
	
	int New(int x) {
		len[++tot] = x;
		return tot;
	}
	
	void Build() {
		New(0), New(-1);
		fail[0] = 1;
		s[0] = -1;
	}
	
	int Find(int x) {
		while (s[n - 1 - len[x]] != s[n]) x = fail[x];
		return x;
	}
	
	void Insert(int x) {
		s[++n] = x;
		int cur = Find(Last);
		if (!trans[cur][x]) {
			int now = New(len[cur] + 2),
			tmp = Find(fail[cur]);
			fail[now] = trans[tmp][x];
			sum[now] = sum[fail[now]] + 1;
			trans[cur][x] = now;
		}
		Last = trans[cur][x];
	}
}

参考资料

EOF

评论

暂无评论

发表评论

可以用@mike来提到mike这个用户，mike会被高亮显示。如果你真的想打“@”这个字符，请用“@@”。

博客信息

作者
Jayun
时间
2022-11-22 21:35:43
博客类型
文章
标签