以下介绍的有自动机的思想,但不一定是自动机。
Manacher
可以以 $\mathcal{O}(n)$ 的时间复杂度求出字符串关于回文子串一类的问题。
令字符串 $s=\texttt{bbdkd}$ 。
在这里面,有偶回文子串 $\texttt{bb}$ 、奇回文子串 $\texttt{dkd}$ ,在计算的过程中还要对奇偶问题进行讨论太过于麻烦,所以可以在每个字符之间加入特殊字符(首尾特殊字符可以作边界):
$$s'=\texttt{\$\#b\#b\#d\#k\#d\#@} $$
再设 $R_i$ 表示以第 $i$ 位字符为中心的最长回文的半径。对应上面的 $s'$ 可以得到:
$$R=\{1,2,3,2,1,2,1,4,1,2,1\} $$
可以发现,以 $i$ 为中心的最长回文子串长度就是 $R_i-1$ 。
我们在求解 $R$ 数组的过程中再设 $p,mx$ 分别表示当前回文子串中心和回文子串的右端点。若正在计算 $R_i$ ,令 $i$ 关于 $p$ 的对称点 $j=2p-i$ 。然后为了先给 $R_i$ 定下界,进行分类讨论(结合图片思考):
- $mx\leq i$ ,因为恒有 $R_i\geq 1$ ,所以 $R_i$ 下界是 $1$ 。
- $mx-i>R_j$ , $j$ 的左端点没有包裹住 $p$ 的左端点(即以 $j$ 为中心的回文子串被包含与 $p$ 的)。因为是对称点,所以以 $i$ 为中心的回文子串也一定被包含与 $p$ 的,所以 $R_i$ 下界为 $R_j$ 。
- $mx-i\leq R_j$ , $j$ 的左端点包裹住了 $p$ 的左端点(即以 $j$ 为中心的回文子串不被包含与 $p$ 的)。因为不被包含,所以不能保证在 $mx'$ 以前的字符和 $i$ 的对应,所以下界是 $mx-i$ 。
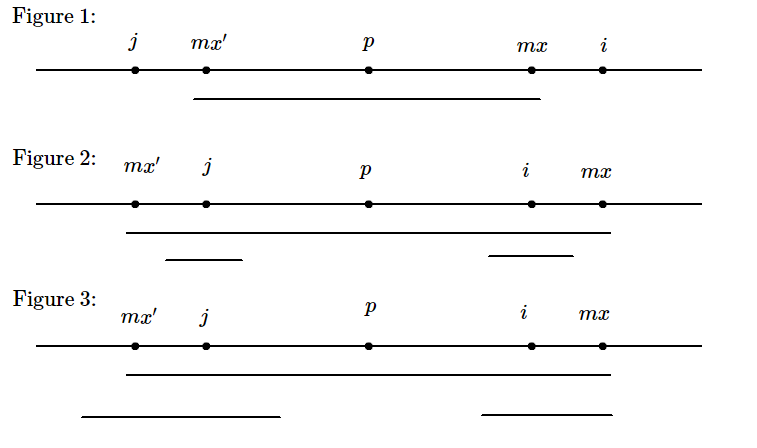
简单来说,定下界就是取 $\min(mx-i,R_j)$ 。
定完下界后,再往两边枚举检测一遍。
由于向左右拓展成功必然会导致 $mx$ 向右移,而 $mx$ 向右移不超过 $n$ 次,故向左右拓展操作的总时间复杂度是 $\mathcal{O}(n)$ 。枚举 $i$ 也是 $\mathcal{O}(n)$ 的,那么 Manacher 算法时间复杂度是 $\mathcal{O}(n)$ 。
int p = 1, mx = 1;
for (int i = 1; i <= n; i++) {
R[i] = min (mx - i, R[2 * p - i]);
while (s[i - R[i]] == s[i + R[i]]) ++R[i];
if (i + R[i] > mx)
mx = i + R[i], p = i;
}
Z 函数
有这样一个数组 $z$ ,其第 $i$ 项的值是字符串 $s$ 和 $\mathrm{suf}(s,i)$ 的最长公共前缀长度(特别地,令 $z_0=0$ )。Z 算法,或称扩展 KMP 算法,可以以 $\mathcal{O}(n)$ 的时间复杂度求解出来。
国外一般称之为 Z Algorithm,而国内则称为 扩展 KMP。
匹配段
对于 $i$ ,把区间 $[i,i+z_i-1]$ 称作匹配段(Z-Box)。可见,我们的目的就是要把每个 $i$ 的匹配段求出来。
求解时中我们维护右端点最靠右的匹配段,记其为 $[l,r]$ 。求解到 $i$ 时,
-
若 $i\leq r$ ,根据定义, $s_{i\cdots r}=s_{i-l\cdots r-l}$ 。则此时 $z_i$ 的下界就为 $\min(z_{i-l},r-i+1)$ 。
- 若 $z_{i-l}<r-i+1$ ,相当于直接可以把当前的 $i$ 转到 $i-l$ 去做,则 $z_{i}=z_{i-l}$ 。
- 若 $z_{i-l}\geq r-i+1$ ,此时 $i$ 不能简单转到 $i-l$ ,因为不能保证 $s_r$ 和 $s_{r-l}$ 往后相同。那就往后朴素枚举即可。
-
若 $i> r$ ,朴素枚举。
void exKMP(char s, int *z) {
int len = strlen(s), l = 0;
z[0] = 0;
for (int i = 1; i < len; i++) {
if (l + z[l] > i) z[i] = min(z[l] - i + l, z[i - l]);
while (i + z[i] < len && s[z[i]] == s[z[i] + i]) z[i]++;
if (i + z[i] > l + z[l]) l = i;
}
}
