题目大意

在平面直角坐标系中，有 $n$ 个圆。需要找到一个方向，使得从原点按该方向射出的一条射线，每隔距离 $d$ 为一个点，这些点落在圆的个数最大（同一个圆可以贡献多次）。

$n\leq2\times10^4,5\leq d\leq10.$

思路

考虑一个圆被以原点为圆心、半径为 $k\cdot d$ 的若干个圆交。如下图。

发现每一个在圆内的弧线的贡献都是 $1$ ，那么就把弧区间化：把每个弧与圆的两个交点与 $x$ 轴的弧度求出来（即把点转到极角坐标，取其弧度），然后差分即可。

至于弧度的求法，先用反正切求出圆心的弧度 $\alpha$ ，见下图：

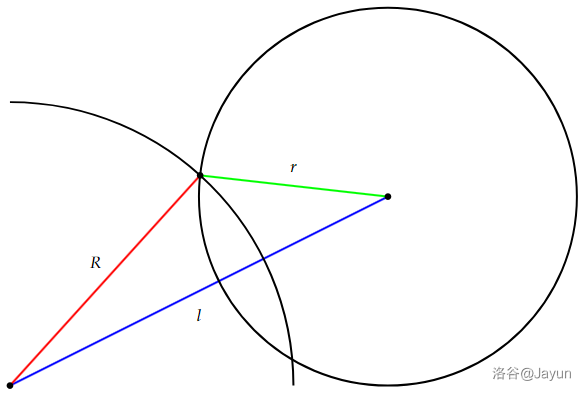
由于 $R,l,r$ 已知，显然可以用余弦定理求得 $\cos\theta=\dfrac{R^2+l^2-r^2}{2Rl}$ ，用反余弦就可以求 $\theta$ 了，那么弧度的区间就是 $[\alpha-\theta,\alpha+\theta]$ ，注意判断 $2\pi$ 边界情况。

代码

const int N = 2e4 + 10;
const long double pi = acos(-1), eps = 1e-5;

inline ll Read() {
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

namespace Main {
	
	int n, d, cnt;
	
	long double rL[N * 10], rR[N * 10];
	
	inline long double Abs(long double a) { return a < 0? -a: a; }
	
	inline void addRange(long double l, long double r) {
		rL[++cnt] = l, rR[cnt] = r;
	}
	
	void Work (int R, int x, int y, int r, long double alpha, long double l) {
		long double theta = acos((R * R + x * x + y * y - r * r) * 1.0 / (2 * R * l));
		if (alpha - theta < eps) {
			addRange(alpha - theta + 2 * pi, 2 * pi - eps);
			addRange(0, alpha + theta);
		} else if (2 * pi - (alpha + theta) < eps) {
			addRange(alpha - theta, 2 * pi);
			addRange(eps, alpha + theta - 2 * pi);
		} else addRange(alpha - theta, alpha + theta);
	}
	
	int main () {
		n = Read(), d = Read();
		for (int i = 1; i <= n; i++) {
			ll x = Read(), y = Read(), r = Read();
			long double l = sqrt(x * x + y * y), alpha = atan2(y, x);
			if (alpha < 0) alpha += 2 * pi;
			ll intL = ceil(l);
			int nearD = intL - intL % d;
			if (Abs(nearD + d - l) < Abs(nearD - l)) nearD += d;
			
			for (int R = nearD; Abs(R - l) <= r; R += d) {
				Work(R, x, y, r, alpha, l);
			}
			for (int R = nearD - d; Abs(R - l) <= r; R -= d) {
				Work(R, x, y, r, alpha, l);
			}
		}
		sort (rL + 1, rL + 1 + cnt);
		sort (rR + 1, rR + 1 + cnt);
		int ans = 0, tmp = 0;
		for (int i = 1, j = 1; i <= cnt && j <= cnt; ) {
			for (; rL[i] <= rR[j] && i <= cnt; i++, tmp++);
			ans = max(ans, tmp);
			for (; rR[j] <= rL[i] && j <= cnt; j++, tmp--);
		}
		printf ("%d\n", ans);
		return 0;
	}
}

int main () {
//	freopen(".in", "r", stdin);
//	freopen(".out", "w", stdout);
	Main::main();
	return 0;
}