题目描述

一个 $n\times m$ 数独是一张包含 $m\times n$ 个区域的网格，其中每个区域包含 $n\times m$ 个格子，因此一个 $n\times m$ 数独共有 $nm\times nm$ 个格子。 $n\times m$ 数独的每行、每列、每个区域都恰好包含 $[1,nm]$ 的所有整数。

对于某行或某列，从某个方向开始，依次列出这行（列）的 $nm$ 个数字，记得到的序列的第一个数为 $X$ ，则称这行（列）在这个方向上的 $X-sum$ 为此序列的前 $X$ 个数之和。

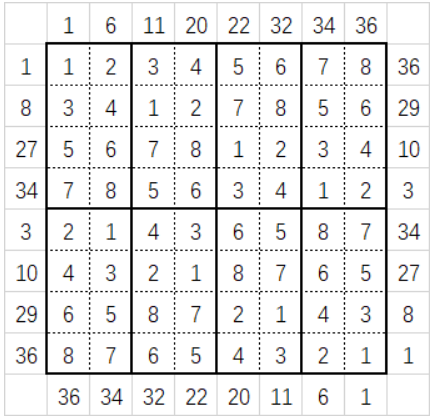
上图列出了一个 $4\times 2$ 数独及其所有 $X-sum$ 。例如，第 $7$ 行从右至左依次为 $[3,4,1,2,7,8,5,6]$ ，其中第一个数是 $3$ ，则第 $7$ 行的从右至左的 $X-sum$ 为 $3+4+1=8$ 。

给定正整数 $n,m$ ，一个方向 $d$ 和一个下标 $x$ ，求字典序最小的 $2^n\times 2^m$ 数独的第 $x$ 行（列）在方向 $d$ 上的 $X-sum$ 。

记数独 $a$ 的第 $i$ 行第 $j$ 列为 $a_{i,j}$ 。称数独 $a$ 的字典序小于数独 $b$ ，当且仅当存在 $x,y$ ，使得对于所有 $i<x$ 有 $a_{i,j}=b_{i,j}$ ，对于所有 $j<y$ 有 $a_{x,j}=b_{x,j}$ ，且 $a_{x,y}<b_{x,y}$ 。上图即为字典序最小的 $4\times2$ 数独。

题解

考察找规律能力，以及推式子的技巧。

遇到这样一个题，你只能先打表，可以发现：

$$A_{2^na+b,2^mc+d}=(a\oplus d)+2^m\cdot(b\oplus c) $$

显然加法的两边是独立的，行和列的求和是对称的。而对于一列的前缀求和， $c,d$ 固定。分成两部分考虑这个求和：

1. $a\oplus d$ 的部分：
   1. 对于 $A_{2^me+f,y}(e<a)$ 的部分：每个的 $f$ 都是 $2^n$ 种，直接算就好 $\sum_{i=0}^a(i\oplus d)$ 就好，这个可以直接枚举 $i$ 的自由位来算。
   2. 否则，单独算一下就好。
2. $b\oplus c$ 的部分：
   1. 对于 $A_{2^me+f,y}(e<a)$ 的部分，每个 $f$ 对应的 $e$ 都是有 $a$ 种，相当于把 $c$ 的后 $n$ 位变成任意的，求和。
   2. 否则，贡献系数都是 $1$ ，依然是转成算 $\sum_{i=0}^a(i\oplus d)$ 。

复杂度 $\mathcal{O}(n+m)$ 。

代码

const int N = 0;

int t;
ll n, m, x;
string d;
__int128 ans;


inline ll Read() {
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

inline void write(__int128 x) {
     if (x < 0) putchar('-'), x = -x;
     if (x>9) write(x / 10);
     putchar(x % 10 + '0');
}

int main() {
	freopen("sudoku.in", "r", stdin);
	freopen("sudoku.out", "w", stdout);
	for (int t = Read(); t--; ) {
		n = Read(), m = Read();
		cin >> d;
		x = Read();
		if (d == "right") d = "left", x = (1LL << n + m) - x + 1;
		if (d == "bottom") d = "top", x = (1LL << n + m) - x + 1;
		ans = 0;
		x--;
		if (d == "left") {
			ll a = (x & (1 << n) - 1) << m | x >> n;
			ll num = a + 1, cur = 0;
			for (int j = n + m; ~j; --j)
				if (cur + (1ll << j) <= num) {
					__int128 t = 1LL << j;
					ans += ((cur ^ a) >> j << j) * t + t * (t-1) / 2;
					cur += 1ll << j;
				}
			ans += num;
		} else {
			ll num = x + 1;
			for (int i = 0; i < n + m; ++i) {
				int t = i < m? i + n: i - m;
				__int128 c = 1ll << i;
				if (x >> i & 1) ans += c * ((num >> t + 1 << t) + min(1ll << t, num - (num >> t + 1 << t + 1)));
				else ans += c * ((num >> t + 1 << t) + max(0ll, num - (num >> t + 1 << t + 1) - (1ll << t)));
			}
			ans += num;
		}
		write(ans);
		putchar(10);
	}
	return 0;
}